I have used Monte-Carlo Tree Search (MCTS) in several projects up to this point, so I thought I should probably write a short entry on this class of algorithms. First, what are Monte-Carlo algorithms in general? These are algorithms that randomly (according to some distribution) sample some system and use the observed outcomes to infer something about the system. This is a very broad definition, but then MC algorithms are very broad as well. I think the simplest example of a Monte-Carlo algorithm is one to approximate the value of Pi. This can be done by generating random pairs of x,y points, each uniformly distributed in the range -1.0 .. 1.0. The fraction of these points that satisfies the condition x^2 + y^2 < 1 is proportional to the value of Pi. Now this is by no means a quickly converging algorithm or an efficient way of approximating Pi, but I think it is an effective example of a Monte-Carlo algorithm.

Monte-Carlo Tree Search is a class of algorithms for analysing a decision tree, with a typical application being game playing (eg: Chess, Go). In games the decision to be made is which of the available moves will result in the best expected long-term outcome. This decision must take into account future moves by an opponent that is trying to maximise its own outcomes. This decision can be made by expanding a game tree from the current position into the future, and choosing the move that has the best expected outcome. One of the nice features of the MCTS approach to game playing is that it requires very little background knowledge of the game. It is enough to be able to generate legal moves from a given position, and to determine if a given state is a terminal state. With only this basic knowledge, without any heuristics or board evaluation functions, MCTS can perform very well on a wide variety of tasks.

There are several flavours of MCTS, one is known as the Upper Confidence Bound (UCB) MCTS. This approach involves growing a game tree, with each node of this tree corresponding to a state and containing the expected outcome of the node’s children. This tree is generated by performing the following steps:

1. traverse down the current tree (with the current game state at the root) until a leaf node is reached
   • this traversal is random, biased between exploration and exploitation
   • when a leaf node is reached, a random move is made (potentially biased), growing the tree by a single node
   • a playout is then made from this new node, randomly making moves until a terminal state is reached (when an outcome can be assigned)
   • this outcome is then propagated back to the root, modifying the expected outcome of each tree node along the way
   • after many iterations the tree should be deeper around the more promising playouts, and the move from the root resulting in the highest expected outcome is typically chosen by the agent.

This algorithm is represented in the diagram below:

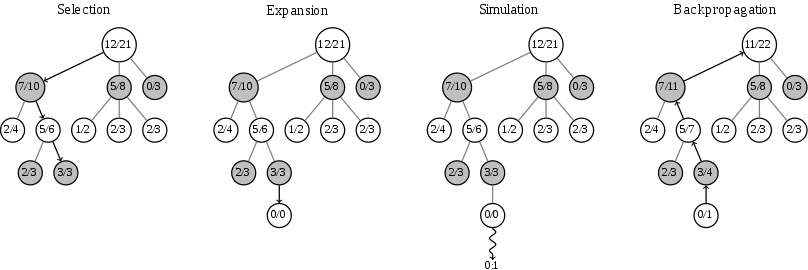
There are a few variations of this basic algorithm. First is the method of choosing which branch of the tree to traverse. This typically involves some kind of exploration-exploitation trade-off. We want to visit the parts of the tree that are known to be good (to search deeper around more promising areas of the tree), but also want to try out different parts of the tree that have not been visited as much (where the estimate of the expected outcome is not as reliable). Second is variations in the playout method. These can be divided into heavy and light playout. Light playout typically involves making random moves until the terminal node is reached. Heavy playout involves using heuristics or some other method of making “smart” moves during playout. There are inherent tradeoffs here and the particular choice will depend on the specific application and domain.

My Applications

So far I’ve used MCTS in two of my projects. One was to play tic-tac-toe versus a q-learned policy (this was mainly the check that the q-learned policy was working well). This worked well enough as an introduction to MCTS in a very simple domain. In another project I implemented a Deep Q-Network to learn to play Connect Four. The output of the network is the q-value of a given action based on a given board state. This allows an agent to play connect-four, but does not explicitly perform lookahead. I then wanted to try using MCTS to add explicit look-ahead to improve performance. In this case the learned q-network was used to both guide the tree expansion and perform early cut-off of the play-out stage. I found that this did not work so well because the evaluation time of the network outweighed any benefits of informed tree expansion and early cut-off. There are two reasons this may have been the case: first is that the implementation was relatively naive and could have been much more efficient (neural-network board evaluation was using the CPU rather than GPU), the second is that for a game like connect-four it may be neural-network guided MCTS does not provide the benefit over uninformed MCTS to outweigh the intrinsic added computation cost.

MCTS For Go

I don’t know the exact details of how the AlphaGo algorithm works (so what I write here may not be totally correct), but I believe it was based around a combination of MCTS and neural networks. Go is a game that defies tree search (eg: minimax search) based on board evaluation functions, due to the nature of the game. MCTS based algorithms have been very successful in this domain, culminating this year in AlphaGo defeating a top ranked professional player (Lee Sedol). From what I know, AlphaGo consists of two separate neural networks that drive a MCTS process. One neural network is trained to predict the likelihood of a player playing a particular move given some board configuration. This is used to guide the tree expansion of the MCTS. Another network is trained to output the probability of winning from a given board configuration. This is used to do early cut-off when performing play-out.

The code for the projects mentioned above can be found on Github: here and here (warning: code is experimental and may be slightly messy).