After playing around with the basics of reinforcement learning, I wanted to try something more advanced. The table based approach I used for Tic-Tac-Toe and a simple Grid World does not scale to more complex domains. The main reasons is that by using a table to represent the Q-value function you cannot generalise. You have to perform numerous explicit samples of a given state-action pair to have a reasonable estimate of its q-value. For a game like 3x3 Tic-Tac-Toe this is possible. But moving up to even a moderately more complex game like connect-four requires much more computation, as there are just too many possible state-action pairs to explicitly represent and explore in a reasonable time.

One possible approach has been to use a linear model to approximate the q-value function. This certainly has better generalisation than a table based approach, but is still fairly restrictive. Neural networks were proposed as a more powerful alternative, but training them has been a problem. Reinforcement learning is by nature episodic and the states observed by the agent are highly correlated. This high correlation would cause problems if the observed states were naively used as direct training input, as the IID assumption is violated. The other issue is the feedback effect due to using the network itself to specify the desired output for a given input. The way q-learning update works is the Q(s,a) value is shifted toward [r + argmax Q(s’, a)]. That is, the value of an action a in a state s should be the direct reward gained plus the maximal action value in the successor state. So the network update is expressed in terms of its own output (albeit for a different state). The feedback effect can make this sort of update unstable. However, Deep Mind recently published a paper on “Deep Q Learning”, where they present a technique to solve these problems and allow effective use of neural networks for q-learning. The target application used by Deep Mind is playing Atari games, but that domain would require a convolutional neural net too large for me to train on my machine. Instead I decided to apply the Deep Q Learning approach to the game of connect four.

Connect Four

Connect Four is a fairly simple game, quite similar to Tic-Tac-Toe in principle. The game has 2-players and the board is traditionally 7x6 squares. Players make alternating moves, dropping their token onto a chosen column. The token ends up in the first unoccupied row above a previously placed token. The first player to have a run of 4 tokens in a row (vertical, horizontal, or diagonal) wins. In total, for a 7x6 board, there are 4,531,985,219,092 possible positions. Clearly too many for a table representation of the q-value function.

Deep Q Learning

There are two main features of deep q-learning that allow neural networks to be effectively used to learn a q-function. The first is the use of experience memory and playback. This involves storing an agent’s experiences of the environment and its actions in a memory, and then sampling from this memory when performing learning. This allows a given experience to be used multiple times during learning. In this case, an “experience” is defined as a tuple (s, a, r, s’), referring to the originating state, action taken, reward gained, and resultant state respectively. An additional benefit of this scheme is that the experiences are sampled randomly from memory, rather than sequentially, which restores the IID assumption of learning. This scheme is in contrast to simply taking an agent’s experience in the environment and feeding it straight into the learner, which would a) only use each specific experience once, and b) the sequence of experiences would be highly correlated. The second feature of “Deep Q Learning” is to use a separate copy of the neural network as the “target” network, and only update it periodically (basically replacing it with the copy of the current “learning” network). The “target” network in this instance is responsible for providing the argmax Q(s’, a) value for Q-learning. So we fix this target network, and every 10,000 (for example) updates of the learning network we update it with the most recent version of the learning network.

Generating Experiences

The overall system can be viewed as two separate parts. One that samples from the experience memory and uses this data to learn a Q-function; and another that actually generates these experiences by interacting with the environment. In this case we play out game of Connect Four to generate the experiences necessary to learn. I tried several different approaches, from playing against an agent that makes random moves, to playing against yourself, to playing in a tournament style set up where each participant is a learning agent. In the end I found that the best bang for buck is playing against yourself, but with a few caveats. The biggest one was making sure the experiences generated are well distributed across the state space. Specifically, when I was training an agent by playing itself, it was performing quite poorly against a random opponent at the conclusion of training. It took me a while to figure out that this was due to a very poor/biased sampling of the state space during training. Basically, each self-play game was starting from the empty board, and then the proceeding play-out followed the policy of the agent (with some randomness). This meant that the game trees that it saw were directly determined by which moves the player made, and thus the learned neural network simply had no idea how to deal with some of the ‘tactics’ employed by say a player making random moves. The simple solution to this problem was to perform self-play starting from a random valid board configuration, rather than from the empty board. This allowed the agent to see a much wider variety of board states during training, yet still train against an intelligent opponent (as compared to training vs random moves).

Board State Encoding

Another implementation issue that was quite important to performance was how to encode the board state as neural network inputs. There are a few options and its not necessarily obvious which is best. One option is to encode each cell as a separate input, with say 1.0 representing a cell with your token, 0.0 an empty cell, and -1.0 a cell with the opponents token. This would give a network with 42 (7x6) inputs and 7 outputs. Another option is to use 1-hot encoding, where each cell is represented by 2 inputs, with one of them being 1.0 and the other 0.0, depending on which player has their token on in the cell, and both being 0.0 if the cell is empty. This gives a network with 84 inputs and 7 outputs. Long story short, it turns out that using the second method was much better than the 1.0,0.0,-1.0 encoding. This is probably because the network has a few more degrees of freedom and does not need to do extra work to “decode” the 1.0,0.0,-1.0 encoding of a cell.

Iterated Training

A key contributor to the final quality of the trained network is how the sample experiences are generated. I experimented with several approaches. The simplest is to play against an opponent that plays random moves. Doing this will result in a network that plays ok, but is used to the opponent making sub-optimal moves most of the time, and thus it will take strange risks. A better alternative is to play against yourself, and learn from these generated experiences. The advantage here is that your opponent (being yourself) is constantly learning and trying to take advantage of your weaknesses, which forces you to adapt and fix these weaknesses in your own strategy (q-function approximation). I saw one potential problem with this approach, and that is the possibility of chasing your own tail. So the resulting network may be constantly learning to beat itself, but as a result forgetting to beat an older version of itself. This was a hypothetical problem, but one way I thought of preventing this possibility is to divide training into episodes, and during every episodes the currently learning player would play against itself, as well as the players from from previous episodes. In this way, every successive training iteration would have the learning network playing against better and better opponents (as well as itself). I hoped that this would result in a better network than simply playing against yourself. Note that for every iteration the learning player is randomly initialised, but the opponents from previous iterations are fixed.

Evaluation

I evaluated the performance of the deep q-learning by graphing the win percentage vs learn iterations of the q-network against a random and min-max players. The iterations on the x-axis don’t take into account the batch size of each learn iteration, so this aspect is a bit meaningless but also not too important. The performance is also measured for separate training episode iterations as well, the hope was that more episode iterations would result in a better q-network player. The results are presented below (note the min-max player is third-party code and can be found here):

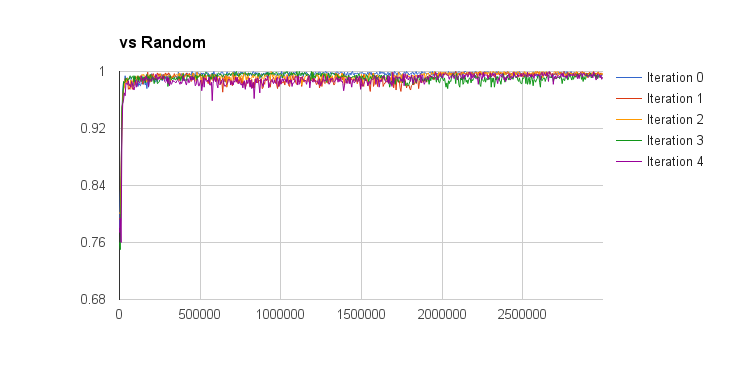
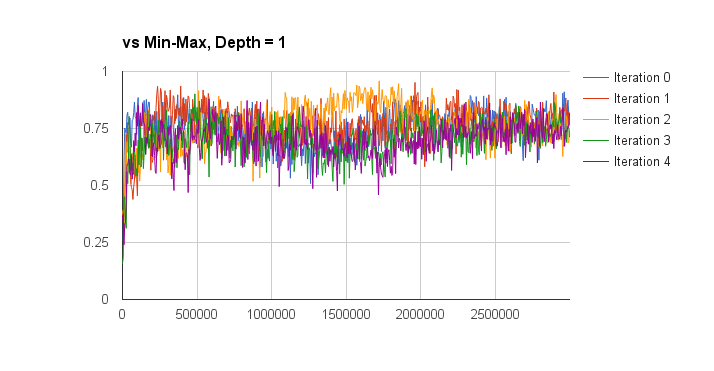
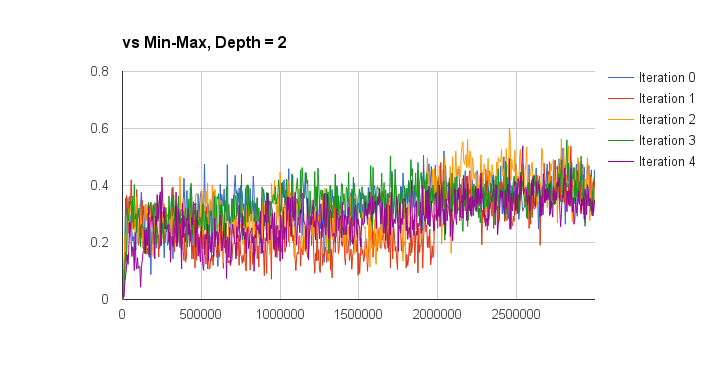
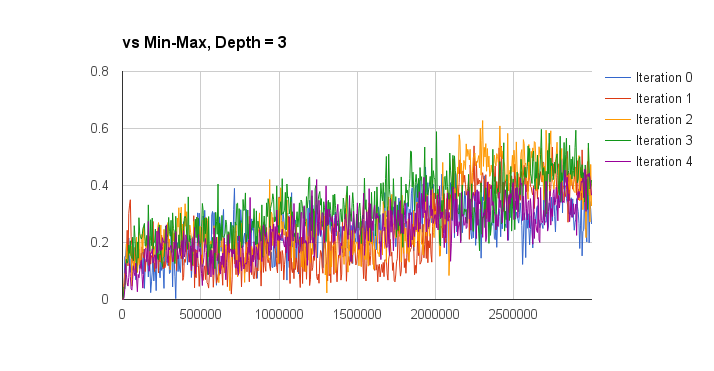
So looking at these results I think I can conclude that iterated training doesn’t result in an obvious increase in q-function quality (proper statistical analysis would be good for this, but I’m lazy). I can also conclude that the trained q-network is much better than random (a low bar, I know), and is approximately equal to a min-max player with a look-ahead of depth 2 (I only plotted the winning percentage here, without accounting for draws). Against look-ahead 2 the q-network wins approximately 45% of games, loses 45% of games, and draws approximately 10%. Against a depth 3 look-ahead player it wins about 40% of the time, and loses about 58% of the time. Not too bad given that the q-network doesn’t do any explicit look-ahead.

Monte-Carlo Tree Search

Using a neural net to model the q-function and then decide moves on the current game state is clearly a fairly limiting approach in general. To perform at the highest level on a game like Connect Four you need to perform some type of look-ahead. One way is to use a monte-carlo tree search combined with the DQN to either limit the search depth or to guide the tree expansion. At a high level this is close to how AlphaGo works (the Go AI that beat Lee Sedol). I played around with this concept a little bit, but not enough to get better performance than a straightforward MTCS that uses random-playout. Definitely something to look into in the future.

The code for this project can be found on Github: here (warning: code is experimental and may be slightly messy).